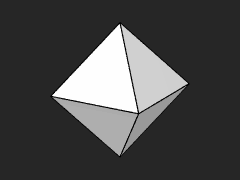
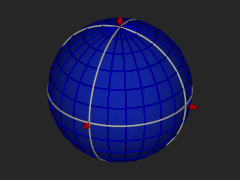
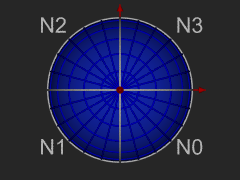
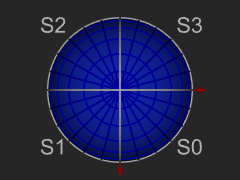
The octahedron and 3 views of its projection onto the sphere.
The latest version discussed here takes advantage of all the latest technologies, and is implemented in C#. The legacy version is still available for historical reasons.
If you are an experienced SDSS Database programmer and don't want to read through the tutorials, some of these links will jump to specific topics of interest
Click for: CURRENT NEWS
These pages will take you to a brief overview of the Hierarchical Triangular mesh, and in turn guide you through its use. You will find more about these topics: (some are not yet completed, and are flagged as such). Check the NEWS link often, this is where critical updates will be posted
The Hierarchical Triangular Mesh is a multi level, recursive decomposition of the sphere. It start with an octahedron, let this be level 0. As you project the edges of the octahedron onto the (unit) spehere creates 8 spherical triangles, 4 on the Northern and 4 on the Southern hemispheres. Four of these triangles share a vertex at the pole. The sides opposite the pole form the equator. You can imagine these by orienting a regular octahedron so that two of its vertices are at the poles, and the other 4 are equally spaced on the equator. The spherical polygons are the projection of the edges of the octahedron onto the circumscribing sphere. See these diagrams::




The 8 spherical triangles N0 - N3 and S0 - S3 represent respectively the 4 northern and southern spherical triangles. We call these level 0 trixels. Each trixel can be split into four smaller trixels by introducing new vertices at the midpoints of each side, and adding a great circle arc segment to connect the new vertices with the existing one. Trixel division repeats recursively and indefinitely to produce smaller and smaller trixels.
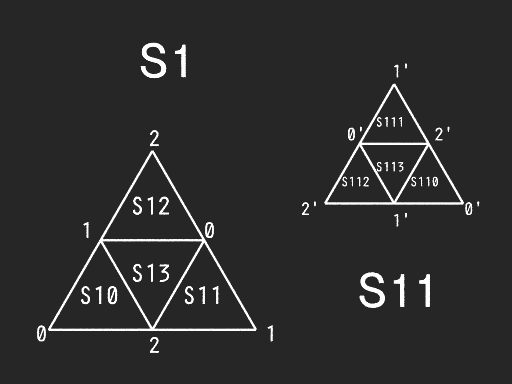 |
This subdivision scheme suggests a natural way of labeling (naming) the trixels.
Each trixel has three vertices labaled 0, 1 or 2.
The opposite midpoints are labeled 0', 1' and 2', respectively.
The newly created trixels receive a label formed by the
name of the parent appended with one of {0, 1, 2}, indicated by the vertex shared with the parent.
The central trixel is suffixed with a '3'. Smaller trixels have longer names.
The length of the name of the trixel also indicates its level.
Points in this decomposition are represented by a leading 1 bit
and then the level 0 trixel number [0..7] and then the successive
sub-trixel numbers [0..3]. This gives each trixel and its center-point
a unique 64 bit identifier, called an HTM ID (HtmID) that represents a
particular trixel in the HTM hierarchy.
|
The smallest valid HtmID is 8. Though the division process can continue indefinitely, the 64-bit representation runs out of bits at level 31. Level 25 is good enough for most applications about 0.6 meter on the surface of the Earth or 0.02 arcseconds. Note, that this numbering scheme is not a complete cover on the positive integers, and not all bit patterns form valid HtmID numbers.
The library supports three coordinate systems: (1) LatLon is the Greenwich Meridian spherical coordinate system of latitude and longitude (lat, lon) used by geographers; (2) J2000 or Equatorial is the celestial right ascension and declination (ra, dec) spherical coordinate system used by astronomers (the vector pointing at the center of the Milky Way defines the intersection of the J2000 prime meridian with the J2000 equator); and (3) Cartesian is a the unit vector representation of a sphere, a point on the sphere (either LatLon or J2000) has a corresponding unit vector. The north pole is (0,0,1) and the prime meridian's intersection with the equator are at (1,0,0) and (-1, 0, 0)
Every trixel in the mesh at any resolution is represented by a single 64-bit number, called the HtmID. For each location given by a point on the surface of the unit sphere, there is a non-uniqe HtmID representing the trixel at a particular level of interest that contains the point. The mapping is not uniqe, simply because there are infinitely many nested triangles around eny point. But every HtmID represents a unique triangular area on the sphere.
A region can be covered with trixels, though not all of them at the same level. If the inside of the region is larger than a particular trixel, then there is no point in subdividing that trixel. The edges, however, will cause fragmentation and create smaller trixels. In order to deal with HtmIDs of variable level trixels, we may stick to a fixed level for representing all trixels without generating every trixel on that level. In our application for practical consideration, this level is set at 20. Therefore all trixels at levels less than 20, can be tiled with a set of level 20 trixels. It turns out, that these HtmID's form a contiguous sequence of numbers. The importance of this is apparent in the discussion of a COVERMAP, but don't go there just yet, except to peek.
in the example below, an HtmID at level 3 is 1023. At level 5, the trixel is subdivided twice, and the HtmID's of all the trixels are in the range 16368 - 16383.
| level 3 | level 4 | level 5 |
|---|---|---|
 |
 |
 |
| 1023 | 4092 - 4095 | 16368 - 16383 |
The level 20 HtmID range is 17575006175232 - 17592186044415. Trivia: the whole sphere has 8 * 4^20 = 8.796e+12 (more than 8 and three quarter billion) level 20 trixels. As 64-bit processors are becoming more mainstream, it is entirely possible, that whole-sphere spatial indexes of spatially organized data can be manipulated in memory soon. When that happens, we already have all that is neccessary to perform image processing on the surfaca of a sphere without projecting to a cartesian plane... but I digress.
So, how do we relate locations to HtmIDs? Very simply, given a level of resolution, you may ask for the HtmID of a trixel that contains your point. In the other direction, the HtmID that represents a trixel is converted to three points that define the corners of the trixel. For complete details, see the (static) methods of the Trixel class.
using Spherical;
using Spherical.Htm;
public class MyClass {
void Func(){
Int64 hid;
double x, y, z;
/* get some values for (x, y, z) so that it is normalized to 1.0
* and compute the hid of the trixel that contains that point at level 12
*/
hid = Trixel.CartesianToHid (x, y, z, 12);
/*
* now, do the opposite (kinda, sorta...), compute the three
* vertices of thetrixel
*/
Cartesian a, b, c;
Trixel.ToTriangle(hid, out a, out b, out c);
}
}