|
|
 Hierarchical Triangular Mesh*
Hierarchical Triangular Mesh*
-
 Description
Description
-
 Documentation / Papers
Documentation / Papers
-
 Implementations / Download
Implementations / Download
*This project is supported by a grant from the NASA AISRP Program.
The Hierarchical Triangular Mesh is the indexing concept used in the
SDSS Science Archive to partition the data by location on the
celestial sphere.
Astronomical data are naturally laid out on a sphere since all objects
have a coordinate to start with. Databases usually split up their data
to cluster objects that are in the same region of the sky. However,
the task of splitting the surface of the sphere into regions turns out
to be a little tricky. People have come up with several schemes how to
deal with it, most of them have problems at the poles or deal with
complicated projection geometry.
The HTM is a simple and elegant way to circumvent this problem. It
does not involve any singularities or deal with projections. Our
implementation is fast enough that computational cost is kept at its
minimum.
We would like to encourage everyone dealing with spherically indexed
data to use the HTM since it is also a great tool to do cross-matching
between databases. The implementation used in the SX is
available to download in C, C++ and Java. A seperate download is
available for SQL Server which gives access to HTM funcitons
inside SQL.
Description
The Hierarchical Triangular Mesh (HTM) is a partitioning scheme to
divide the surface of the unit sphere into spherical triangles. It is
a hierarchical scheme and the subdivisions have not exactly, but
roughly equal areas.
The subdivision starts with the 8 largest equal-sized spherical
triangles: the octahedron on the sphere. These are subdivided
into 4 triangles by connecting the side-midpoints of neighboring
sides. The subdivision may be continued to any level; below we
show subdivisions up to level 5.





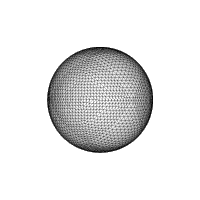
Subdividing the sphere, all triangles planar for simplicity.
Triangle sides are always great circle segments.
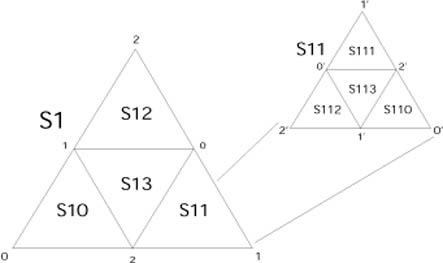
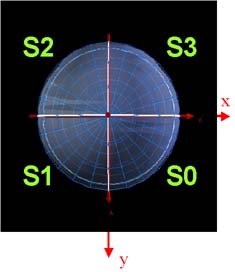
The HTM is stored as a quad-tree, the 8 root triangles are named
N0, N1, N2, N3 and S0, S1, S2, S3. Each node has 4 children, labeled
0-3. In the SX, the database names are the node names at level 5, for
example N201301. N2 is the root name, then
we have 5 digits (01301) denoting which triangle to choose at each level.
The starting 8 nodes and the subdivision scheme.
Further details on how the subdivision is actually performed, querying, cross-matching and statistics can be found in
the documentation.
the folowing table gives an indication of pixel area and number of htm leaves in HTMs of given depths. Pixel areas are not equal so the given number is nominal.
| Level | Area (arcmin^2) | Num Leaves |
| 10 | 1.77E1 | 8,388,608 |
| 11 | 4.43E0 | 33,554,432 |
| 12 | 1.11E0 | 134,217,728 |
| 13 | 2.77E-1 | 536,870,912 |
| 14 | 6.92E-2 | 2,147,483,648 |
| 15 | 1.73E-2 | 8,589,934,592 |
| 20 | 1.69E-5 | 8,796,093,022,208 |
| 25 | 1.65E-8 | 9,007,199,254,740,922 |
|




 Hierarchical Triangular Mesh*
Hierarchical Triangular Mesh*




